2021학년도 수능 가형 20번 어려운 이유 & 해설
2021학년도 수능 가형 20번 (by.csm).pdf
안녕하세요 CSM입니다.
20번 해설을 들고왔습니다.
현재 21번보다
체감 난이도가 높다고 여겨지는 20번입니다.
21번
체감난이도가 높은 이유는
1) 함수 g(x)의 치역설정
2) 정적분의 "결과값"을 통해 함수 개형추론
에 있어서 기존 기출에서
단단하게 연습하기 어려운 형태여서
학생들이 조금 풀기 어려워한 듯 보입니다.
먼저 교양적으로 알아야 할 사실은
아래 그림과 같이 삼각함수 반주기의
넓이(정적분값)를 빠르게 파악해야 합니다.
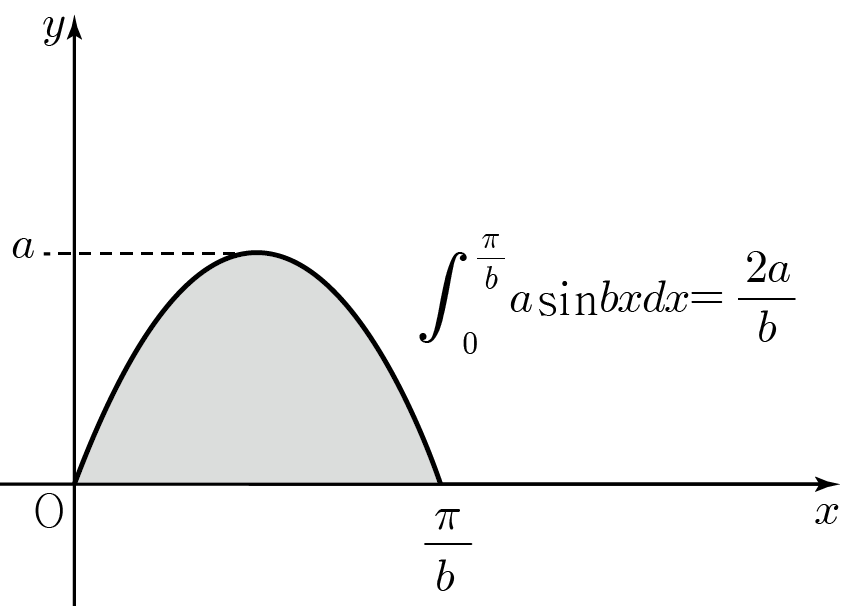
이를 토대로 해설은 다음과 같습니다. (아래 이미지 PDF도 첨부)
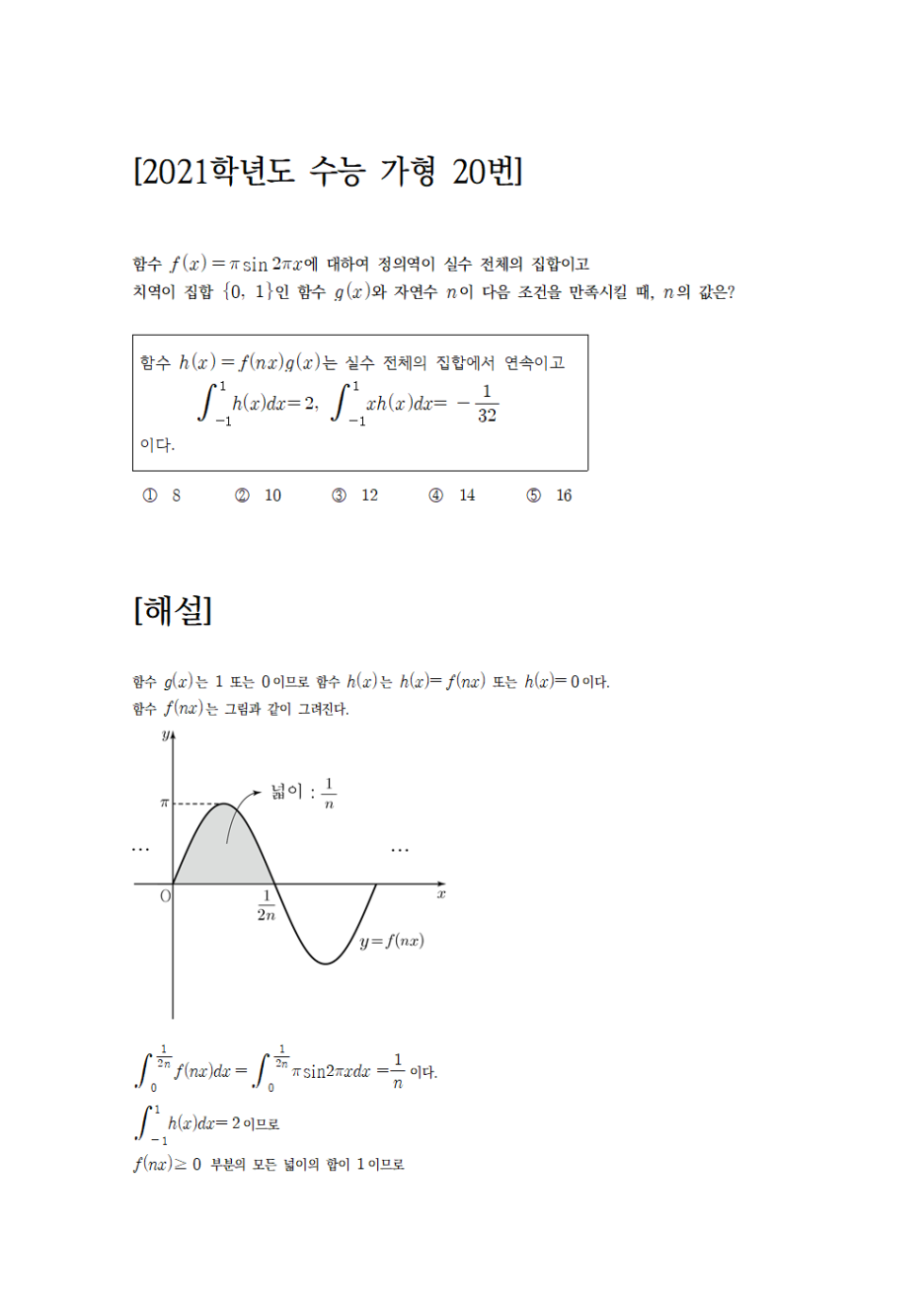
사진 설명을 입력하세요.
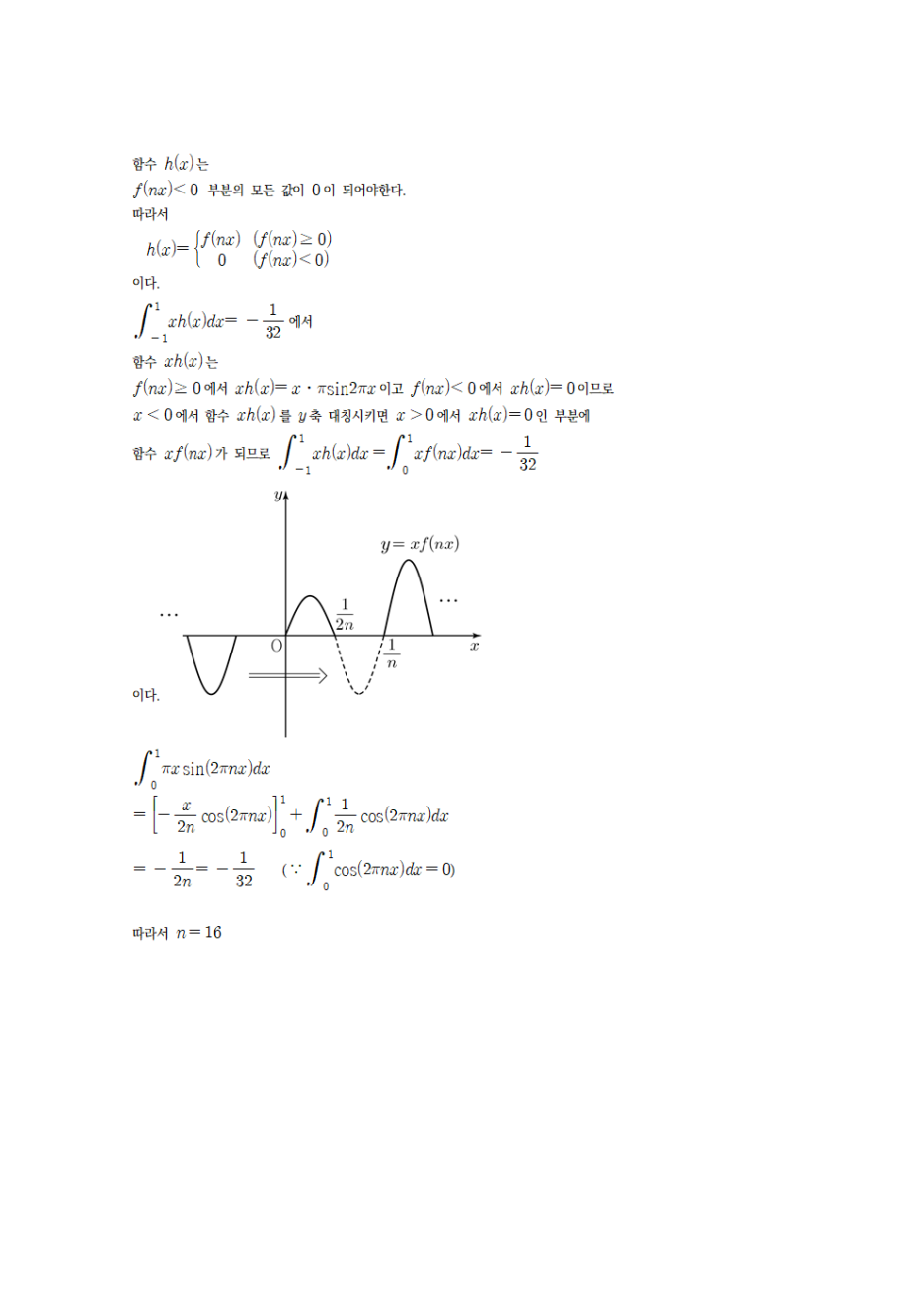
사진 설명을 입력하세요.
두가지 적분의 해석을 넓이관점과 식의 관점으로 보는 방향에 따라
풀이속도가 달라질 수 있는 문제이고 이런 경우에는
학생들에게 체감난이도 격차를 줄 수 있었던 문제라고 생각합니다.
도움이 되셨기를 바랍니다.
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
생1->생2 4
로 바꾸려고 하는데 어떻게 생각하세요 제가 생1을 정말 못해서요
-
유급만은 안됨
-
신호등 되게 감성적으로 생기지 않았나요 약간 도시감성
-
티원 내려치는 놈들보면 대가리를 내려치고 싶음
-
고민이네요 ㅜ
-
여름에 학교에서 똥싸다가 모기 30번 넘게 물리고 그거 반정도가 흉터로 남아서 보기싫게생김 ㅇㅅㅇ
-
어제 혼자 간 숙소 일회용품 중 콘돔이 있길래 물풍선으로 만들어서 던지고 놀다...
-
이거 수학적으로 중요한 건가요? 의미있는건가요?
-
캬캬캬
-
수능 목적이 아니라하면 풀면 좋을까요?
-
경북대 합격생을 위한 노크선배 꿀팁 [경북대 25] [기숙사별 장단점부터 생활 꿀팁] 1
대학커뮤니티 노크에서 선발한 경북대 선배가 오르비에 있는 예비 경북대학생, 경북대...
-
진짜 뭐임? 지방 약수고 15명정도 뽑는 과긴 한데 뭐지 내 데이터상 칸수가 올라가는일은 없었는데
-
ㅇㅈ 2
를 보며 눈호강을 하는 나
-
개념완성 교재 작년이랑 많이 다른가요? 작년 교쟈 써도 되나요?
-
ㅇㅈ 0
영정사진(였던것) 지금 딴과목들 보면 이정도면 관짝 열고 다시 부활한듯
-
건대 기준 5, 6칸 다 노랑, 연초 나오는데
-
찾고 싶어도 찾을 수 없는 것(근대 이전) -> 찾고 싶으면 노력이 필요하지만 찾을...
-
에휴다노
-
ㅇㅈ 5
아니 이거 왜 경제가이겨
-
경험당임
-
파콜 다 해주는게 맞죠?
-
나도인증할래 11
아무리 열심히 찍어도 못생기게 나왔어 그냥 내 손이 못생긴 건가?
-
저 오늘 납치삘 나는 추합 당했는데 2차부턴 추합 잘 안도나요?? 차라리 더 높은데...
-
빅뱅 이전의 상태는 현재 과학의 영역에서 명확히 다루기 어렵기 때문에, 철학과...
-
ㅈㄴ 뜯었거든요ㅎㅎ
-
제발 연대로 가주세요 ㅠㅠ
-
손 ㅇㅈ 4
제 손목 둘레는 16cm에요
-
자기가 aa bb cc 뭐 받았는지는 모르는건가요??
-
사탐런고수님들 1
생윤이 올해처럼 또 안나올거같은데 불과탐 확정이니 그냥 지구 하나 껴서 사문지구가...
-
그런 가능성은 없는걸까요? 문과라서 잘 모르겠네요
-
최근 들어서 살이 좀 붙었는지 원래 입던 바지인데도 빵댕이가 꽉차서 자꾸 눈길이 갔음;;
-
이신혁t 아폴로 0
다 하는데 보통 얼마나 걸리나요??
-
생1 - 보이면 ㅈㄴ 쉬움 바로 풀림, 근데 안보이면 멍때림 생2 - 보는건...
-
ㅇㅈ 13
나머지는새벽에 근데어짜피님들내얼굴다알잖아
-
동국대vs건대 6
동국대 전전,건대 재료공 둘다 붙으면 어디감?
-
군면제인 덕에 사수까지하고..물론 재수 나이 때부터 공부 시작하긴 했지만..
-
이제까지 단 한명도 없었다는..
-
경제보다 경영이 사기업 취업에서는 유의미하게 유리한듯 0
같은 상경계로 묶이긴 한다만 배우는 과목도 그렇고 학회 활성화 정도도 많이 차이남...
-
손 크기는 모르겠고 11
남르비 중에서 나보다 발 작은 사람은 없을 것 같음
-
화생에서 생지 0
약대가고싶은데 생명 사문 보단 생지가 낫겟죠? 근데 사문 만점이어도 생지가...
-
스1 어싸 받을 수 있나요?
-
18살도 뽑아주나 개학 전까지 100마넌만 벌어보고 싶은데
-
나도 손 ㅇㅈ 5
-
이과긴한데 뭔가 숫자를 다루는 문과 일을 하고 싶어요(재무, 금융 등) 한양대 가서...
-
외로워요 25
친구들이 저랑 안 놀아줘요ㅠㅠ
-
맡긴 결과:
-
반수하게되면 입학전까지는 여기 다닐건데 보통 얼마 하는지 궁금해서요
-
실수로 이름을 까버려서.. 재업합니다! 오르비언들은 반 값에 침 놓아 드립니다ㅎㅎㅎ...























































개인적으로 매우 친숙한 유형은 아니라고 생각합니다. 현장기준 어려웠을 것 같아요
asinbx 한칸넓이 a/b라서 n이 2의거듭제곱만 될거같아서 1.5중에 고민하고 5번 왼쪽정적분으로 계산해보니 사인 양수는 0곱해서 없어질것같고 음수는 -1곱해져서 양수가 될것같은 느낌으로 킹리적갓심씀
ㄹㅇ 걍 찍맞이네
아니에요 킹리적갓심은 절대 그냥 나오지 않습니다. 잘하셨습니다 ^__^
해설 잘 봤어요. 마지막에 정적분 int_{-1}^{1} xh(x)dx=int_{0}^{1} xf(nx)로 넘어가는 부분이 잘 이해가 안되는데 혹시 여유있으시다면 설명해주실 수 있을까요? 저는 사진처럼 풀었는데, 계산이 무척 더럽고 현장에서 저렇게 풀면 계산실수가 반드시 있을 것 같아서 부탁드립니다....(첫 줄의 오류는 건너뛰어주세요 고치기 귀찮아서...ㅎㅎ)
in_{-1}^{0}xh(x)dx 부분만 관찰해주시면 될 것 같습니다. 함숫값이 음수인 부분은 제거 되었을것이고 양수인부분만 남은 h(x)에 대하여 x를 곱하는데 x<0이므로 xh(x)<0가 됩니다.
따라서 xh(x)를 (-1,1)에서 그린 후 각각 적분을 하여도 괜찮습니다만,
(-1,0)인 부분을 그대로 y축 대칭시켜보면 결국 xf(nx)가 완성된다는 것을 알 수 있습니다.
이는 f(nx)가 처음부터 대칭함수이고 x를 곱하여서 '대칭성질'이 남아있다고 생각하여 판단할 수 있으며 이를 (-1, 0) => (0, 1)로 이동하는 치환적분하여 식적으로도 설명가능하나 이를 계산으로 의도하기보다는 최근 "영역관찰"을 포인트 잡아왔기에 그림도 적절히 섞어서 확인해주시면 될 것 같습니다.^^
아아아아 다 그대로 대칭되니까 그렇겠네요 감사합니다.
찍는게 더 빠를 듯. 2랑 1/32 나오고 f(nx) 주기가 1/n 이니까 8, 16 처럼 2의 거듭제곱꼴로 나오는 수가 답일 것 같고 8은 너무 작아서 16했는데 아.. 계산이 엄청 빡센거였네요
진짜 시험장에서 제일 어려웠어요... 30 20 이 최고봉.
이제 21 29 은 킬러 아닌듯해여ㅜ
와.. 그냥 1/2n~1/n, 1/n~3/2n 계속 적분해가면서 귀납적으로 적분값을 찾아냈는데 y축대칭하면 한번의 적분으로 풀리네요 진짜 충격이네