"Chapter. 0 - 함수의 연속"
“Chapter. 0 – 함수의 연속”
안녕하세요 ‘한국외대 부’입니다. 언제나 여러분 입시에 가장 먼저 앞서있고,
길을 내주는 길잡이가 되어드리도록 최선을 다해 앞장서겠습니다!
오늘의 제목은 “함수의 연속”입니다. 모든 칼럼은 저의 자료의 내용으로 진행됩니다!
수2 내용의 함수 파트는 22번 15번 등으로 킬러로 자주 등장하는 내용입니다.
오늘은 킬러로 자주 등장하는 ‘함수의 연속’에 대해 알아봅시다.
함수의 연속은 함수를 결정하는데 중요한 조건이 됩니다.
수2에선 초월함수가 등장하지 않아 ‘연속’이라는 조건 만으로도 많은 정보를 알 수 있습니다!
특히, 수2에선 다항함수가 자주 출현하기에 연속과 미분 가능성에 대해서 항상 주의깊게 확인해야합니다.
연속임을 확인하는 방법은 정말 단순합니다.

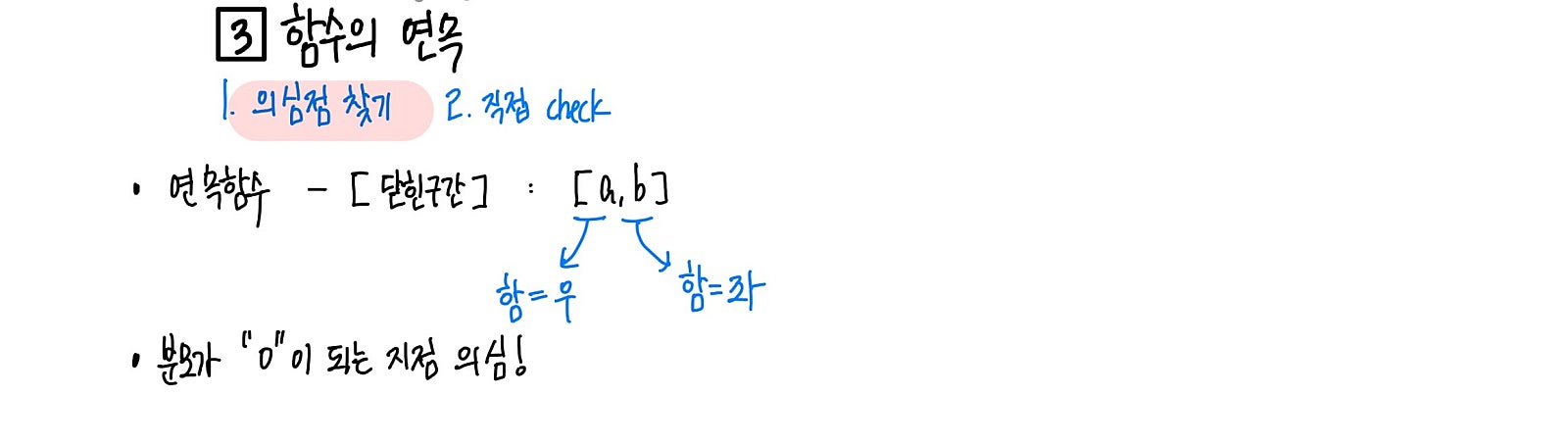
함수의 연속을 확인하는 의심점 찾는 방법을 확인해주세요.
먼저, 의심되는 지점에서 연속이 되는지만 확인하면 됩니다!
그 의심되는 지점을 어떻게 찾는지 알아봅시다.
첫 번째, 경계를 의심하자!
단순히 설명된 연속함수의 경우 닫힌 구간으로 정의된 그 경계가 의심점이 됩니다.
경계로 정의된 함수의 경우 경계 사이는 대부분 연속되는 구간으로 주어지고 그 경계에서 다른 함수로 바뀌거나 새로운 조건이 붙는 경우가 많습니다.
두 번째, 분모가 “0”이되는 지점을 의심하자!
분수로 표현된 유리함수의 경우 분모가 0인 지점을 항상 의심해야 합니다.
그 지점은 존재 자체를 안하기에 분모가 0이되는 좌,우 극한의 값과 같은 값을 지니는
다른 함수의 값으로 표현되어야 연속이 됩니다.
마지막으로, 합성함수의 연속에 대해 알아봅시다!

합성함수는 그 주인공이 무조건! 겉함수입니다.
그림과 함께 보면 합성함수는 두 개의 함수를 합성 시켜놓은 꼴이기에
두 개의 함수의 연속 의심지점을 모두 고려해야 합니다.
따라서 이와같이 속함수에서 겉함수로 넘어가는 부분을 꼼꼼히 체크해야합니다.
어느하나 빠지지 않게 잘 체크하여 그 좌,우극한 값과 함수값이 같은지 확인해야합니다.
합성함수의 연속을 잘 이해했나 확인해보기 위해
2016년 6월 모의고사 문제를 예시로 같이 풀어봅시다.


앞의 합성함수의 연속을 확인 하는 방법을 같이 보면서 해설을 읽어주세요!
속함수의 연속의 조건에서 경계인 x=1에서의 좌,우,함수값을 모두 의심해야하며,
그 값을 정의역으로 하는 g(x)에서의 값이 모두 동일해야하니
g(a)값은 g(1)의 값과 같아야 합니다, 따라서 이를 만족시키는 a의 모든 값의 곱은 1과 –1의곱인 –1입니다.
합성함수를 관찰할 때 중요하게 봐야하는 부분은
속함수의 치역이 겉함수의 정의역이 된다는 점입니다.
이점은 아직 미숙할지 몰라도 여러 예시 문항들을 풀어보면서 꾸준히 연습해야 합니다.
오늘의 내용은 여기까지 입니다!
앞으로 더 많은 내용들로 꾸준히 찾아올테니 좋아요과 구독 한번씩만 눌러주시고 기다려주세요!
자료의 전체버전은
https://cafe.naver.com/suhui/28704323 에서 확인해주세요!
고민이나 공부상담, 원하시는 칼럼의 내용이 있으시면 댓글이나 쪽지로 남겨주세요.
다음 칼럼에 반영하여 작성하겠습니다!
수험생의 길잡이가 되어드리는
'한국외대 부'였습니다 감사합니다!
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-

 좋아요 0 답글 달기 신고
좋아요 0 답글 달기 신고
-
윗표본인데 왜 연경을쓰지 저걸로..?
-
그룹 아이브 멤버 장원영에 대한 가짜뉴스 유포 혐의로 사이버 렉커 유튜버 탈덕수용소...
-
만19세 이상 8
중에 중앙대 모르는 사람 얼마나될까? 재명이가 인지도 ㅈㄴ끌어올릴거 같긴한데
-
지문 분석하고 어느 부분에서 문제화 됐는지만 체크하고 넘어갑니다 문학처럼 세세하게...
-
이런거 사두는거 좋아해서 있는데 박근혜는 말아먹었고.. 문재인꺼는 가격오를까
-
존나게 낑낑대면서 풀었는데 일어나보니 내용이 기억이 안나네... 아까워라
-
대통령 체포됫구나 16
이거 탄핵되고 이재명 대통령될 삘인데 아 빨리 국장 처분하고 집사야하는데 아파트...
-
닥공은 1
언제나 진리..
-
서울대 1차합격자 점공 거의다 들어왔다던데, 펑크날 것같은 학과가 있나요? 6
설대 1차 합격자의 점공이 거의다 들어온 상태라 펑크날지 여부도 지금쯤이면 윤곽이...
-
강의 중간에 끊기고 잠적해야됨?
-
박광일 기출분석 방법 영상 업로드됨 ㄱㄱ링 홀수 드가자~~~~
-
가능한가요? 뒷통수 심한가요
-
전 정치를 잘 몰라서 딱히 지지하는 사람이 없는디..
-
슬슬 헤어밴드로도 커버가 안 되는군
-
중대발표 9
2시였던가 조발 가능성 없음?
-
진짜네
-
국민의힘 틀딱들이 윤석열 지휘아래 지랄한거임 보수에 이준석말고 자유주의적인 성향...
-
어디까지준거지
-
시시시호의 기하과외 28
-
왜 윤석열을 체포할때는 절차를 싸그리 무시하는거죠?
-
우리 귀여운 오댕이나 봐요。◕‿◕。
-
저번처럼 이대남들이 국힘 몰빵하면 민주당 답없는거아닌가 그냥 이재명 구할라고 쇼한거임?
-
일본 초밥 먹음 6
음식 사진 찍는 건 까먹음
-
계속 정치글만 봤더니 힘드네
-
국어-1월안에 수국김 끝내고 2월에 일클래스 들어가기 수학-1월까지 수분감 최대한...
-
와
-
윤석열은 처음부터 싫었음 보수의 적통이 아님
-
이재명은 멀쩡히 불구속 수사 재판 받고 조국은 12심 실형받고도 총선나오고+당선되고...
-
수능끝나고 76-77이였는데 기분이 좋아요..
-
15일 내란 우두머리 피의자 윤석열 대통령 2차 체포영장 집행을 막아선 국민의힘...
-
훠훠 0
훠어
-
민주당or국힘 지지자면 그짝 애들이 뭔 지랄을 해도 다 빨아주는 거. 아무리...
-
민생얘기는 뒷전 둘다 좆임
-
제가 대한민국 반장이 된다면 오뿡이들에게 1억씩 뿌리겠습니다 감사합니다
-
제발
-
"따흐흑...윤 총장님 감사합니다..."
-
그냥갈라치기당하고좌파우파로나뉘고지역감정생기고하루종일쳐짜우는것만보면정내미가다떨어져서정치...
-
이번 수능 진짜 개망해서 기숙학원에서 거는 성적제한에 다 걸려요... 조건 안에 못...
-
어제 입고라면서 아직 발송시작 안했네
-
운동완뇨 5
ᕦ(ò_óˇ)ᕤ 몸짱이될거야
-
문학론 끝나고 유네스코가 맞나요?아님 병행이 맞나요?
-
카톡 검열 궁금한게 23
신고식 운영이면 내가 아무나 신고 때려도 그 사람 검열할 수 있는 거 아님? 오뿡이...
-
24년도 엑셀러레이터
-
조중동+종편은 착한아이 컴플렉스에
-
정치글 한 번만 6
안녕하세요 조정치입니다
-
검열과 감시가 싫다고하면 “ㅋㅋㅋ 왜 님 혹시 범죄자?” ㅇㅈㄹ 하는게 문재임...
-
정경심 “조국 영치금, 현금은 안 돼…계좌나 우편환으로” 10
수감 중인 조국 전 조국혁신당 대표의 부인 정경심 전 동양대 교수가 조 전 대표에게...
-
학력이 같음뇨









































